Doğrusal ve Doğrusal Olmayan Devreler

[Abyss]

Herkese mrb, cok bir sorum olacak:

Elektronikte sıklıkla karşıma çıkan ama basit bir tanımını bilmeyip tüm araştırmalarima rağmet internette net bir cevabini da bulamadığım bir soru, basit bir soru...

"Doğrusal (lineer) devre nedir? Doğrusal olmayan (lineer olmayan) devre nedir? Bunların birbirinden farkı nedir? "

Net bir açıklama yapacak arkadaşa çok minnettar olacağım. Teşekkür ediyorum.

 

[taydin]

Aşağıda güzel bir tanımlama yapılmış:

Linear and non-linear network circuit - Semiconductor for You

Linear and non-linear network circuit:-A Linear circuit is one whose parameters are constant with time and they do not change with voltage or current and circuit obeys Ohm’s Law. A Non Linear circuit is that circuit whose parameters change with voltage or current and circuit does not obey Ohm’s Law.

www.semiconductorforu.com

"Lineer devre, parametreleri zamanla, voltajla veya akımla değişmeyen ve Ohm kanununa uyan devredir."
"Lineer devrelere örnek olarak direnç, direnç devresi, indüktör ve endüktif devre, kapasitör ve kapasitif devre verilebilir."

"Lineer olmayan devre, parametreleri zamanla, voltajla veya akımla değişen ve Ohm kanununa uymayan devredir."
"Lineer olmayan devrelere örnek olarak diyot, transformatör, demir nüve, indüktör, transistör verilebilir."

Yalnız yukarıdaki sitede indüktör hem lineer olan hem de lineer olmayan devre elemanlarına örnek olarak verilmiş. Buradaki ayrıntı şudur: Nüvesi olmayan bir indüktör lineer devre elemanıdır. Ama histerezis etkisi ve belli bir akımdan sonra oluşan satürasyon etkisi nedeniyle nüveli indüktörler nonlineer devre elemanlarıdır.

 

[Harmonik]

LİNEAR = DOĞRUSAL
NON-LİNEAR = DOĞRUSAL OLMAYAN

Pekala bu doğrusallık nerden geliyor ;
Genel olarak doğrusal kelimesi, köşegene benzeyen düz bir çizgi anlamına gelir ve gerilim ile akım arasındaki doğrusal özellikleri anlatır. yani devredeki akım akışı, voltajla doğru orantılıdır. Voltajda bir artış varsa, devredeki akım akışı da artar ve bunun tersi de geçerlidir. Doğrusal devrenin çıkış özellikleri, aşağıdaki şekildeki akım ve voltaj arasındadır.

Doğrusal bir devrede, çıkışın tepkisi girişle doğru orantılıdır. Devrede 'f' frekansına sahip uygulanan sinüzoidal ve çıkış, iki nokta arasındaki voltajın da sinüzoidal frekansa 'f' sahip olduğu anlamına gelir.

Doğrusal olmayan devrede, çıkış karakteristiği, aşağıdaki şekilde gösterildiği gibi voltaj ve akım arasında bir eğri çizgisi gibidir.

Eğitim ve öğretimde ezberciliğe oldum olası karşı biriyimdir olayın özüne kökenine inip mantığını kavramayı severim.

 

[Abyss]

Tüm bunlardan şöyle bir sonuç çıkıyor:

Direnç, nüvesiz bobin ve kapasitor gibi elemanların bulundugu doğrusal devreler parametreleri zaman, akım ve gerilim gibi niceliklere göre değişmeyen, basit yani süperpozisyon teoremi gibi devre çözüm yöntemleri kullanılarak çözülebilen ve ohm kanununa uyan devrelerdir...
Doğrusal devrelerde voltaj ile akım arasında doğrusal bir ilişki mevcuttur yani voltaj artarsa akimda orantılı olarak artar yada voltaj azalırsa akımda onunla birlikte ayni oranda azalır.

Buna karşın diyot, transistör, transformatör ve demir çekirdekli yani demir nüveli bobin gibi devre elemanlarina sahip doğrusal olmayan devreler ise sahip olduğu çeşitli parametreler zaman, akım, gerilim gibi niceliklere bağlı olarak değişiklik gösteren ve ohm kanuna uymayan, yapısal ve elemansal iceriklerinden dolayı kompleks yani süperpozisyon gibi devre çözüm yöntemleriyle kolayca çözülemeyen devrelerdir.
Doğrusal olmayan devrelerde ise voltaj ve akım arasında doğrusal olmayan yada başka bir tabirler eğrisel (parabolik) bir orantı vardır yani voltaj artisi yada azalisiyla akimdaki degisim ayni oranda değildir.

Böylelikle bu sorun kesin olarak eğer hiç bir üstadın itirazi yok ise çözüme kavuşmuş oluyor. Konuyla ilgili bilgi arayan bir çok elektrik-elektronik teknikeri için faydalı bir içerik foruma kazandirilmiş oldu diye düşünüyorum. Herkese tekrar teşekkürlerimi sunuyorum, ayrıca yorum paylaşmak isteyen herkes ekleme yada düzeltme yapabilir, konu açıktir.

 

[taydin]

Parabolik dememek lazım. Parabolün anlamı bellidir, ikinci derece bir fonksiyonu temsil eder [imath]f(x) = ax^2+bx+c[/imath]

 

[Abyss]

Doğrusal olmayan devrelerdeki elemanların kendilerine uygulanan elektriksel uyartımlara zaman çerçevesinde cevabı eğrisel nitelikte, burda kesinlik var ancak grafığe bakarsak parabolik yerine yarı parabolik daha anlaşılır görünüyor doğru. O şekilde düzeltebiliriz.

 

[Endorfin35+]

Doğrusal olmayan devreleri neden ohm kanununa uyduramadık?

 

[Abyss]

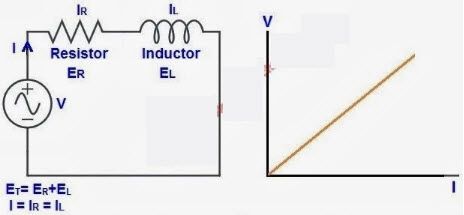
Ohm kanunu temel bir doğa kanunu degildir, yalnızca elektriksel açıdan ele alındığında Gerilim, Akım ve Direnç arasındaki doğrusal ilişkiyi V = I x R biçiminde ifade eder.

Bu yasa bir elektrik devresinin incelenmesinde en temel yasadır. Basit bir biçimde ifade etmek gerekirse örneğin bir doğrusal devre elemanı olan direncin uçları arasındaki elektriksel potansiyel farkı (V), direnç üzerinden geçen akım (I) ile doğru orantılıdır ve orantı sabiti direncin (R) sabit olan değerini verir.
Ohm kanununa göre direnç üzerinden geçen akım arttıkça, direncin uçları arasındaki potansiyel farkta direncin değerini sabit bırakacak biçimde artar, örneğin 3 Ohm'luk bir direnç üzerine 6 Volt gerilim uyguluyorsak;

V = I x R
6 = I x 3
I = 2 Amper olacaktır.

Eğer burada gerilimi 6 Volt yerine 12 Volt olarak tatbik edersek; yani iki katına çıkarırsak, yine ohm kanununa göre:

V = I x R
12 = I x 3
I = 4 Amper olacaktır.

Her iki deneydede ayni 3 ohm sabit değere sahip direnci kullandik, gerilimi tam iki katına çıkardığımızda akımda aynı oranda iki katına çıktı. Farklı gerilim değerleri için deneyi sürekli tekrarlayıp bununan akım karşiliklarıni not eder ve bunun V/I grafigini çizersek bu bize doğrusal bir grafik verir ve bu grafigin eğimi yani grafik üzeri deki herhangi bir nokta için karşı/komşu ( Tanjant) ifadesi direncin değerine eşittir.

İşte doğrusal (lineer) devre elemanlari bu mantikla çalışan ve dogrusal devreler dedigimiz yapıları olusturan elemanlardir. Direnç gibi doğrusal bir devre elemanı aşağıdaki iki özellige sahiptir:

I-)HOMOJENLİK, eger elemanın girişi bir sabit ile çarpılır veya bölunürse çıkışida ayni sabitle çarpılmış yada bolünmüş olur.
II-)TOPLAMSALLIK, dogrusal bir elemana uygulanan girişlerin toplamı; girişlerin elemana ayri ayri uygulanması durumundaki toplama eşittir...

Grafikten doğrunun eğiminin her noktada aynı olduğu görulecektir...Bu aynı olan egim direncin degeridir...

6/2=3
12/4=3
18/6=3
24/8=3

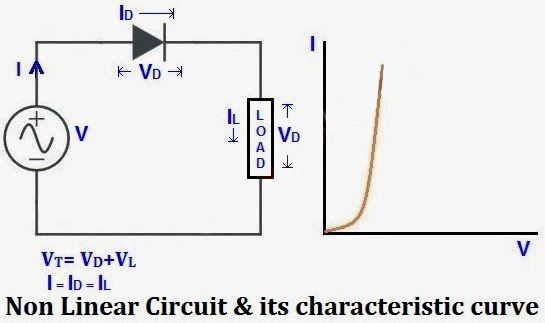
Yukarıdaki basit deneylerde ayni 3 ohmluk direnci kullandik, dolayisiyla uygulanan gerilime gore akımdaki değişim doğru orantiliydı (direncin değerini değiştirecek örneğin ısı gibi ufak etkenleri gozardi edilmişti) ancak bazı devre elemanlarinin örneğin diyot gibi direnc değerinin, yarı iletken yapı içeriği nedeniyle, sabit olmadığıni biliyoruz. Diyot yalnızca bir yönde akım geçiren devre elemanıdır, bir yöndeki direnci ihmal edilebilecek kadar küçük, diğer yöndeki direnci ise çok buyuk olan devre elemanidir.

Bu tür elemanların üzerine aynı yukardaki deneyi uyguladıgimizda dogru orantisal akım değişimlerini alamiyoruz. Onun yerine elde ettiğimiz gerilim-akım degerleriyle cizdigimiz grafik egrisel gorunümde oluyor. Bu elemanlarin direnc degerlerinin sabit olmamasını ise örneğin diyotlardaki V/I grafigi cok güzel acıkliyor; bilindiği üzere diyotlarda kırılma adinda bir kavram var eger elimizdeki silisyum bir diyot var ise bunu dogru yonde akımı iletebilmesi için 0.7 volt gerilim uygulanmasi gerekiyor. Bu deger bir iletim bariyeri, aşmadan diyotu iletime geçiremiyorsunuz...

Grafige göre iletim bariyerini aştığınızda akim inanilmaz değisimler ( yukselisler ve düşüsler) gosteriyor ve buda elemanin ohm kanununa riayet etmemesine neden oluyor...

Özetle bir nonlineer eleman olarak diyot uzerinden kısaca özetleyecek olursam; Sızinti akimi, kırilma gerilimi gibi elemanin kendine has, yari iletken yapısindan ileri gelen çeşitli davranışsal ozellikleri ohm kanununa uymamasina neden oluyor. dogrusal olmayan devrelerde dogrusal olmayan eleman icerikleri nedeniyle dogal olarak ohm kanununa uygun hereketler sergileyemiyor....

 

[Abyss]

Georg Simon Ohm, 16 mart 1787 senesinde Earlangen’de dünyaya geldi. Bir çilingirin oğlu olan Ohm, bir süre babasının yanında çalıştıktan sonra Köln’deki Cizvitler Koleji’nde ve Berlin Harp Okulu’nda matematik ve fizik öğretmenliği yaptı. Köln, Nürnberg ve Münih Üniversitelerinde profesörlük görevi aldı.

Daha önceleri Alessandro Volta aracılığıyla bulunan elektro kimyasal hücreler üzerine çalışmaya ve araştırma yapmaya başladı. Kendi donanımını tercih ederek yaptığı araştırmalar sırasında, bir telden geçen akımın geçtiği alanla doğru orantılı ve uzunluğuyla ters orantılı olduğunu buldu. Bu deney sonuçlarını tercih ederek, gerilim akım ve direnç içindeki bağlantıyı çözdü. Bu denklem bi hayli büyük bir gelişmeydi çünkü elektrik devrelerin analizlerinin yapılmasının başlangıcını ve temelini oluşturuyordu. Lakin 1827 senesinde bu buluşunu yayınlayınca, kolejde hoş karşılanmadı ve lise öğretmenliğinden istifa etmeye zorlandı. Bu durum onu yoksulluğa itti.



1833’te Nürnberg’de profesörlük pozisyonuna kabul edilinceye kadar bu yoksul yaşamı sürdü. Üniversitedeki pozisyonu onun için çok iyi bir gelişme oldu.


Elektrik akımını bir sıvının debisi, potansiyel farkını da bir düzey farkı gibi kabullenerek ve elektrik miktarını, şiddetini, elektromotor kuvveti kesin bir biçimde tanımlayarak, elektrokinetik olaylar için bilimsel terimler ortaya koydu. Belirli kesit ve uzunluktaki, belirli bir madenden yapılmış bir teli standart seçerek, öbür teller için bugün ‘direnç’ adı verilen özelliği “indirgenmiş uzunluk” adıyla tanımladı ve ünlü yasasını, “akım şiddeti = elektroskopik kuvvet / indirgenmiş uzunluk” şekilinde açıkladı. 1826’da paylaşımı yaptığı makalelerde, Ohm’un bu yasaya tümüyle deneysel yoldan vardığı görülür.

Ohm’un bulduğu ve bugün Ohm Kanunu olarak anılan,

I = V / R

Üç değişkenli formül, tüm elektrik devrelerinin temelini oluşturmaktadır. Bu buluşundan sonra bir elektrik devresinde elektromotor gücünün dağılımını keşfetti. Direnç, elektromotor kuvveti ve akım şidddeti içindeki bağlantıyı buldu.

1830’da Becquerel’in çalışmalarından habersiz olarak pillerdeki kutuplama olayını açıkladı. 1843’te insan kulağının çeşitli titreşimler içinde, sinüsoidal titreşimleri ayırt ederek algılayabileceğini ispatladı. Ayrıca canavar düdüklerinin teorisini kurdu.

Georg Ohm, 6 Temmuz 1854 tarihinde Münih’te öldü.
Yaşamı sırasında bilime yaptığı katkı takdir görmeyen George Simon Ohm, ölümünden hemen hemen 30 yıl sonra adı direnç birimine verilerek onurlandırıldı.

Bu ünlü ve değerli bilim insanının biyografisinide paylaşmak istedim.

Kaynak: www.biyografisi.org

 

[taydin]

Doğrusal olmayan devreleri neden ohm kanununa uyduramadık?

Biraz zorlarsan aslında Ohm kanununa uydurabilirsin, ama gerçek hayatta işe yarayan birşey olmaz.

Mesela diyelim ileri yönde diyoda 0.65 V verdik ve i₁ akımı geçiyor. Sonra diyelim gene ileri yönde 0.75 V verdik ve i₂ akımı geçiyor. Bu iki durum için direnci hesaplarsak, farklı çıkacaktır. Yani diyodun direnç değeri sabit değil, voltaja göre değişiyor, dinamik bir direnç değerine sahip. Sırf Mr Ohm'u memnun etmek için bu dinamik dirence göre gidebilirsin, ama burada pratikte bir yarar elde etmek mümkün değil