asicocuk34
Aktif Üye
- Katılım
- 1 Kasım 2022
- Mesajlar
- 234
[imath]1-0.\overline{9}=x[/imath] dediğimizde x'in 0'dan daha büyük olduğu bir değer elde edemessek buna nasıl matematik diyebiliriz? sizce de bir noksanlık yok mu? bende bu hataya düştüm. o yüzden bu yazımda, hatalarımı düzeltelerek hangi mantık üzerinde kurduğumu ve yanıldığım noktaları tekrar aynı konu üzerinde düzenlemeler yaparak anlatıyorum. sizde bu hataya düşmeyin. boşuna vaktinizi öldürmeyin.
[imath]1/3=0.\overline{3}[/imath] 'a eşit olmadığını düşündüm.
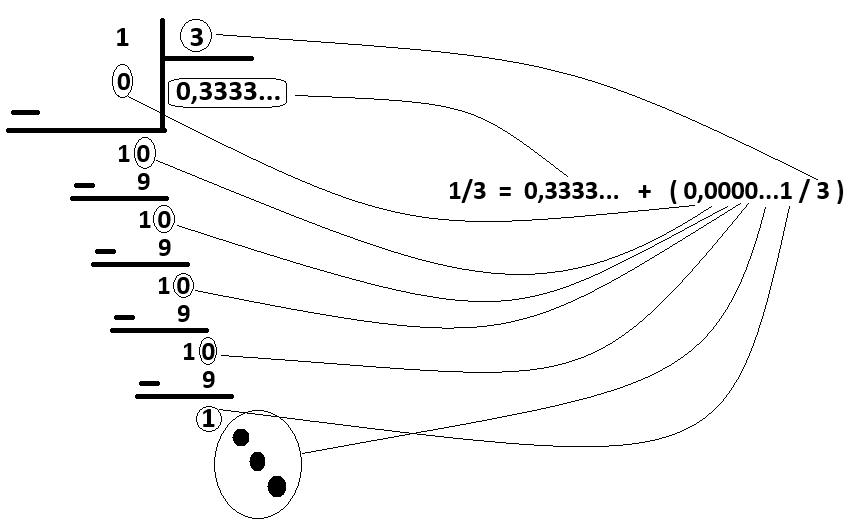
1 sayısını 3'e böldüğümüzde aslında çıkan sonuç 0,3333... değerine kalan dahil edilmediğin için tam olarak eşit değil gibi geliyor. kalan değer "0,0000...1" tür. bölme işlemini ne kadar yaparsan yap "0,0000...1" yani [imath]0.\overline{0}1[/imath] değeri bölünemediği için kalıyor.. zaten tam bölünemediğin için devirli sayı diyoruz.bu mantık üzerinde işlemelere devam edelim...
[imath]1/3=0.\overline{3}+(0.\overline{0}1/3)[/imath]
[imath]0.\overline{0}1[/imath] sayısında sonsuz tane 0 demek yerine "n" kadar bilinmeyen basamağında 0 rakamı olan bir sayıdır. devirli bir sayı değildir. ve oluşturduğum değer son basamağının 1 olmasının zorunlu olduğunu ifade eden mantıksal bir değerdir. bu kuralı ben oluşturdum. çünkü bu bana göre daha mantıklı geldi ve sonuçlar doğru çıkıyor.
[imath]0.\overline{3}*3=0.\overline{9}[/imath]
[imath]1=1.\overline{0}[/imath]
[imath]1=1.\overline{0}0[/imath]
[imath]1.\overline{0}0-0.\overline{9}9=0.\overline{0}1[/imath]
[imath]x=[0.\overline{3}+(0.\overline{0}1/3)]*3[/imath]
[imath]x=(0.\overline{3}*3)+[(0.\overline{0}1/3)*3][/imath]
[imath]x=0.\overline{9}+0.\overline{0}1[/imath]
[imath]x=1[/imath]
[imath]0.\overline{0}1[/imath] değeri 0 dır. çünkü böyle bir sayı yok. yaptığım sadece sonsuz basanaklı bir 0 göstermekten ibaret. yanılmışım.
eğer 10 ile çarpma işlemi yapmaya çalışırsak bu sefer sonunda sıfır bulunan devirli bir sayı elde etmiş olacağız. sayının sonunda sıfır olmak zorunda. bu şekilde kaç basamaklı olduğunu bilmediğimiz bir sayıyı 10 ile çarpabiliyoruz.
[imath]0.\overline{9}*10=9.\overline{9}0[/imath]
burada 0'î etkisiz eleman olarak almıyoruz kendisini de sayıya dahil ediyoruz. 0 sayımızın son basamağındaki değişmez rakamdır. bu kuralı ben koydum.bu şekilde "n" kadar bilinmeyen basamağında 9 bulunan değeri 10 ile çarpmak mümkün olmuş oluyor.
[imath]0.\overline{9}[/imath] sayısının son basamağını, eğer 4 işlem yapıyorsak yazmak zorundayız. bir devreden sayının son basamağı belirtilmemiş ise kendisidir.
[imath]0.\overline{9}=0.\overline{9}9[/imath]
[imath]9.\overline{9}0-0.\overline{9}9[/imath]
[imath]9.\overline{9}0-0.\overline{9}9=8.\overline{9}1[/imath]
işlemi nasıl yaptım? 0 dan 9 çıkmaz 1 onluk alırız komşudan. 10dan 9 çıktı 1 kaldı.komşu 9 du 8 oldu. 8 den 9 çıkmaz. komşudan bir onluk alırız. şeklinde devam ediyor. en sonda 8 den 0 çıktı 8 kaldı.
şimdi matematikcilerin bize anlattığı işlemi kendi kurallarımızla yapalım:
[imath]x=0.\overline{9}[/imath]
bu sayıyı kendi oluşturduğum mantık kuralına göre 10 ile çarpalım:
[imath]10x=9.\overline{9}0[/imath]
o zaman yukarıda ki kendi oluşturduğum çıkartma işlemine göre :
[imath]9x=8.\overline{9}1[/imath]
[imath]x=8.\overline{9}1/9[/imath]
[imath]x=0.\overline{9}[/imath]
İnanmassanız googleye "8,99999991/9" yazın. istediğiniz kadar 9 yazın sonuç 0.9999... olacaktır. hesap makinesi gücü yetmeyince yuvarlayıp 1 diyecektir.
bunun ispat olduğunu düşündüm ama değil.
1/3=0.3333... bu ifade 1/3'ün bölündüğünde çıkan sonucun mantıksal bir ifadesi. neden mantıksal çünkü 1/3'ün hem matematiksel ifadesini taşıyor hemde mantıksal olarak bölünemediğini ifade ediyor.
1/3*3=0.3333...*3
1=0,9999... bu sayıyı görünce sanki 0.0000...1 ekleyince o zaman 1'e eşit olacak gibi gelebilir ama işin mantığı bu sayının tanımını iyi anlamakta. bu sayı soyut bir kavram. 3 tane 1/3 yani 0.3333... mantıksal ifadesinden oluşuyor.
kıymetli matematik hocalarımızın bize gösterdiği kısmi ispat yöntemi:
x=0,9999... bu sayıyı 10 ile çarpıyoruz.
10x=9,9999... oluyor çünkü 0,9999... sayısı sonunda 0 içermeyen son rakamı 9 olmak zorunda olan bir mantıksal ifadedir.
---------------------
9x=9/9
x=1=0,9999...
sonuç olarak, devili sayılarda değil, "n" kadar bilinmeyen basamağı devreden sayılarda işlem yapabilmiş oldum. 9 sayısının sonsuza kadar gitmediği durumu sadece açıklaya bildim. sonsuza kadar giden bir 0.9999... = 1 oluyor. malesef bu yola eşit olamadığı düşünerek başladım ama sonuç olarak eşit olduğunu anladım.
[imath]1/3=0.\overline{3}[/imath] 'a eşit olmadığını düşündüm.
1 sayısını 3'e böldüğümüzde aslında çıkan sonuç 0,3333... değerine kalan dahil edilmediğin için tam olarak eşit değil gibi geliyor. kalan değer "0,0000...1" tür. bölme işlemini ne kadar yaparsan yap "0,0000...1" yani [imath]0.\overline{0}1[/imath] değeri bölünemediği için kalıyor.. zaten tam bölünemediğin için devirli sayı diyoruz.bu mantık üzerinde işlemelere devam edelim...
[imath]1/3=0.\overline{3}+(0.\overline{0}1/3)[/imath]
[imath]0.\overline{0}1[/imath] sayısında sonsuz tane 0 demek yerine "n" kadar bilinmeyen basamağında 0 rakamı olan bir sayıdır. devirli bir sayı değildir. ve oluşturduğum değer son basamağının 1 olmasının zorunlu olduğunu ifade eden mantıksal bir değerdir. bu kuralı ben oluşturdum. çünkü bu bana göre daha mantıklı geldi ve sonuçlar doğru çıkıyor.
[imath]0.\overline{3}*3=0.\overline{9}[/imath]
[imath]1=1.\overline{0}[/imath]
[imath]1=1.\overline{0}0[/imath]
[imath]1.\overline{0}0-0.\overline{9}9=0.\overline{0}1[/imath]
[imath]x=[0.\overline{3}+(0.\overline{0}1/3)]*3[/imath]
[imath]x=(0.\overline{3}*3)+[(0.\overline{0}1/3)*3][/imath]
[imath]x=0.\overline{9}+0.\overline{0}1[/imath]
[imath]x=1[/imath]
[imath]0.\overline{0}1[/imath] değeri 0 dır. çünkü böyle bir sayı yok. yaptığım sadece sonsuz basanaklı bir 0 göstermekten ibaret. yanılmışım.
eğer 10 ile çarpma işlemi yapmaya çalışırsak bu sefer sonunda sıfır bulunan devirli bir sayı elde etmiş olacağız. sayının sonunda sıfır olmak zorunda. bu şekilde kaç basamaklı olduğunu bilmediğimiz bir sayıyı 10 ile çarpabiliyoruz.
[imath]0.\overline{9}*10=9.\overline{9}0[/imath]
burada 0'î etkisiz eleman olarak almıyoruz kendisini de sayıya dahil ediyoruz. 0 sayımızın son basamağındaki değişmez rakamdır. bu kuralı ben koydum.bu şekilde "n" kadar bilinmeyen basamağında 9 bulunan değeri 10 ile çarpmak mümkün olmuş oluyor.
[imath]0.\overline{9}[/imath] sayısının son basamağını, eğer 4 işlem yapıyorsak yazmak zorundayız. bir devreden sayının son basamağı belirtilmemiş ise kendisidir.
[imath]0.\overline{9}=0.\overline{9}9[/imath]
[imath]9.\overline{9}0-0.\overline{9}9[/imath]
[imath]9.\overline{9}0-0.\overline{9}9=8.\overline{9}1[/imath]
işlemi nasıl yaptım? 0 dan 9 çıkmaz 1 onluk alırız komşudan. 10dan 9 çıktı 1 kaldı.komşu 9 du 8 oldu. 8 den 9 çıkmaz. komşudan bir onluk alırız. şeklinde devam ediyor. en sonda 8 den 0 çıktı 8 kaldı.
şimdi matematikcilerin bize anlattığı işlemi kendi kurallarımızla yapalım:
[imath]x=0.\overline{9}[/imath]
bu sayıyı kendi oluşturduğum mantık kuralına göre 10 ile çarpalım:
[imath]10x=9.\overline{9}0[/imath]
o zaman yukarıda ki kendi oluşturduğum çıkartma işlemine göre :
[imath]9x=8.\overline{9}1[/imath]
[imath]x=8.\overline{9}1/9[/imath]
[imath]x=0.\overline{9}[/imath]
İnanmassanız googleye "8,99999991/9" yazın. istediğiniz kadar 9 yazın sonuç 0.9999... olacaktır. hesap makinesi gücü yetmeyince yuvarlayıp 1 diyecektir.
bunun ispat olduğunu düşündüm ama değil.
1/3=0.3333... bu ifade 1/3'ün bölündüğünde çıkan sonucun mantıksal bir ifadesi. neden mantıksal çünkü 1/3'ün hem matematiksel ifadesini taşıyor hemde mantıksal olarak bölünemediğini ifade ediyor.
1/3*3=0.3333...*3
1=0,9999... bu sayıyı görünce sanki 0.0000...1 ekleyince o zaman 1'e eşit olacak gibi gelebilir ama işin mantığı bu sayının tanımını iyi anlamakta. bu sayı soyut bir kavram. 3 tane 1/3 yani 0.3333... mantıksal ifadesinden oluşuyor.
kıymetli matematik hocalarımızın bize gösterdiği kısmi ispat yöntemi:
x=0,9999... bu sayıyı 10 ile çarpıyoruz.
10x=9,9999... oluyor çünkü 0,9999... sayısı sonunda 0 içermeyen son rakamı 9 olmak zorunda olan bir mantıksal ifadedir.
---------------------
9x=9/9
x=1=0,9999...
sonuç olarak, devili sayılarda değil, "n" kadar bilinmeyen basamağı devreden sayılarda işlem yapabilmiş oldum. 9 sayısının sonsuza kadar gitmediği durumu sadece açıklaya bildim. sonsuza kadar giden bir 0.9999... = 1 oluyor. malesef bu yola eşit olamadığı düşünerek başladım ama sonuç olarak eşit olduğunu anladım.
Son düzenleme:

