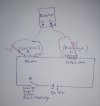
Karmasik bir hesap yok fakat oncelikle uzerinde tartisabilmek icin ortaya ciddi bir devre semasi konmasi lazim. Birinci mesajdaki cizime bakinca gozlerim kaniyor.
Sanirim su sekilde bir duzenek kurdunuz.
22025 eklentisine bak
S=0 da kapanan anahtar T1 suresince kapali kalsin.
[math]i=\frac{V}{R}(1-e^{-\frac{R}{L}t})[/math]
Bu durumda direncte harcanan gucun ani degeri [math]P=R*i^2[/math]
[math]P=R*\frac{V^2}{R^2}(1-e^{-\frac{R}{L}t})^2[/math]
[math]P=\frac{V^2}{R}(1-2e^{-\frac{R}{L}t}+e^{-2\frac{R}{L}t})[/math]
0..T1 araliginda integre edersek direncte isiya neden olan enerjiyi hesaplamis oluruz.
[math]E=\int_0^{T_1}\frac{V^2}{R}(1-2e^{-\frac{R}{L}t}+e^{-2\frac{R}{L}t})dt[/math]
[math]E=\frac{V^2}{R}(t+2*\frac{R}{L}e^{-\frac{R}{L}t}-\frac{2R}{L}+e^{-2\frac{R}{L}t})|_0^{T_1}[/math]
[math]E=\frac{V^2}{R}(t+\frac{2R}{L}e^{-\frac{R}{L}T1}-\frac{2R}{L}+e^{-2\frac{R}{L}T1} - 1 + 1)[/math]
[math]E=\frac{V^2}{R}(t+\frac{2R}{L}e^{-\frac{R}{L}T1}-\frac{2R}{L}+e^{-2\frac{R}{L}T1})[/math]
simdi direncte harcanan gucu bulalum. Bu da E/T1 dir.
[math]P_R=\frac{V^2}{R{T_1}}(t+\frac{2R}{L}e^{-\frac{R}{L}T1}-\frac{2R}{L}+e^{-2\frac{R}{L}T1})[/math]
Bobinde depolanan enerji icin bu kadar eziyete gerek yok. Isteyen hesaplayabilir. [math]E=\frac{1}{2}Li^2[/math]
Bobinde enerji depolamak icin harcanan guc [math]P_L=\frac{1}{2{T_1}}Li^2[/math]
Bu ikisini toplayinca guc kaynagindan 0//T1 araliginda cekilen toplam guc hesaplanmis olur.
Yada [math]P=V*I[\math] den gidebiliriz.
Simdi de ayni islemi RMS degerden yola cikarak sen hesapla.
[math]P_{rms}=\V*I_{rms}[/math]