Mikro Step
Kıdemli Üye
- Katılım
- 25 Eylül 2022
- Mesajlar
- 8,081
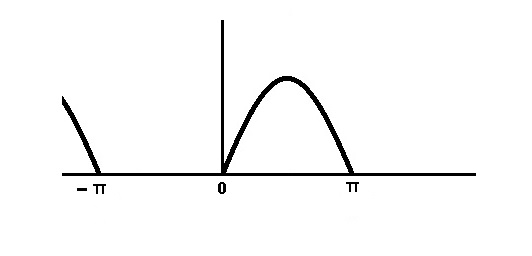
y=sin(x) fonksiyonumuz var.
Bunu yarim dalga dogrulttugumuzda
y=sin(x) {x>=0 ....x<pi}
y=0 {x>=pi ..x<2pi}
olarak yazabiliriz.
Bu fonksiyonun Fourier acilimini analitik olarak yapalim. (Dogrudan sonucu veren matematik sitelerinden yardim almak yerine bu islemleri elle yapacagim)
Ancak o kadar hata yapmaya musait ki cozume ulasmam bir kac gunu alabilir.
[math]A_o=\frac{1}{\pi}\int_0^{\pi}sin(\theta)d\theta=\frac{2}{\pi}[/math]
[math]A_n=\frac{1}{\pi}\int_0^{\pi}sin(\theta)cos(n\theta)d\theta[/math]
[math]sin(a+b)=sin(a)cos(b)+sin(b)cos(a)[/math][math]sin(a-b)=sin(a)cos(b) -sin(b)cos(a)[/math][math]sin(a+b)+sin(a-b)=2sin(a)cos(b)[/math][math]sin(a)cos(b)=\frac{1}{2}(sin(a+b)+sin(a-b))[/math][math]A_n=\frac{1}{\pi}\int_0^{\pi}sin(\theta)cos(n\theta)d\theta=\frac{1}{2\pi}\int_0^{\pi}(sin(\theta+n\theta)+sin(\theta-n\theta))d\theta[/math]
[math]A_n=\frac{1}{2\pi}\int_0^{\pi}(sin((n+1)\theta)-sin((n-1)\theta))d\theta[/math][math]A_n=\frac{1}{2\pi}(-\frac{cos((n+1)\theta)}{n+1}+\frac{cos((n-1)\theta)}{n-1})|_0^\pi[/math][math]A_n=\frac{1}{2\pi}(\frac{cos((n-1)\pi) -1}{n-1}-\frac{cos((n+1)\pi)-1}{n+1})[/math]
n tek ise An=0 oluyor. Dolayisi ile An i sadece n cift degerler icin hesaplayacagiz.
[math]B_n=\frac{1}{\pi}\int_0^{\pi}sin(\theta)sin(n\theta)d\theta[/math][math]cos(a+b)=cos(a)cos(b)-sin(a)sin(b)[/math][math]-cos(a+b)=-cos(a)cos(b)+sin(a)sin(b)[/math][math]cos(a-b)=cos(a)cos(b)+sin(a)sin(b)[/math][math]-cos(a+b) + cos(a-b)=2sin(a)sin(b)[/math][math]sin(a)sin(b)=\frac{1}{2}(cos(a-b)-cos(a+b) )[/math][math]sin(x)sin(nx)=\frac{1}{2}(cos(x-nx)-cos(x+nx) )[/math][math]sin(x)sin(nx)=\frac{1}{2}(cos((1-n)x)-cos((1+n)x))[/math][math]B_n=\frac{1}{\pi}\int_0^{\pi}\frac{1}{2}(cos((1-n)\theta)-cos((1+n)\theta))d\theta[/math][math]B_n=\frac{1}{2\pi}\int_0^{\pi}(cos((1-n)\theta)d\theta-\frac{1}{2\pi}\int_0^{\pi}cos((1+n)\theta))d\theta[/math][math]B_n=\frac{1}{2\pi(1-n)}sin((1-n)\theta)|_0^\pi-\frac{1}{2\pi(1+n)}sin((1+n)\theta))|_0^\pi[/math][math]B_n=\frac{1}{2\pi(1-n)}sin((1-n)\pi)-\frac{1}{2\pi(1+n)}sin((1+n)\pi)[/math]
n=1 icin bir terslik var diger tum n degerleri icin Bn katsayisi 0.
n=1 icin ilk integrali cozelim.
[math]B_1=\frac{1}{\pi}\int_0^{\pi}sin(\theta)sin(\theta)d\theta=\frac{1}{2\pi}\int_0^{\pi}(1-cos(2\theta))d\theta=\frac{1}{2}[/math]
Artik herhangi bir n degeri icin An katsayisini dogrudan hesaplayabiliriz.
[math]A_2=-\frac{2}{3\pi}[/math][math]A_4=-\frac{2}{15\pi}[/math][math]A_6=-\frac{2}{35\pi}[/math][math]A_8=-\frac{2}{63\pi}[/math]
[math]y=\frac{A_0}{2}+\sum_{k=1}^{\infin} A_ncos(k\theta)+\sum_{k=1}^{\infin} B_nsin(k\theta)[/math]
Ilk 8 harmonik icin
[math]y=\frac{1}{\pi}+\frac{1}{2}sin(\theta) -\frac{2}{3\pi}cos(2\theta)-\frac{2}{15\pi}cos(4\theta)-\frac{2}{35\pi}cos(6\theta)-\frac{2}{63\pi}cos(8\theta)[/math]
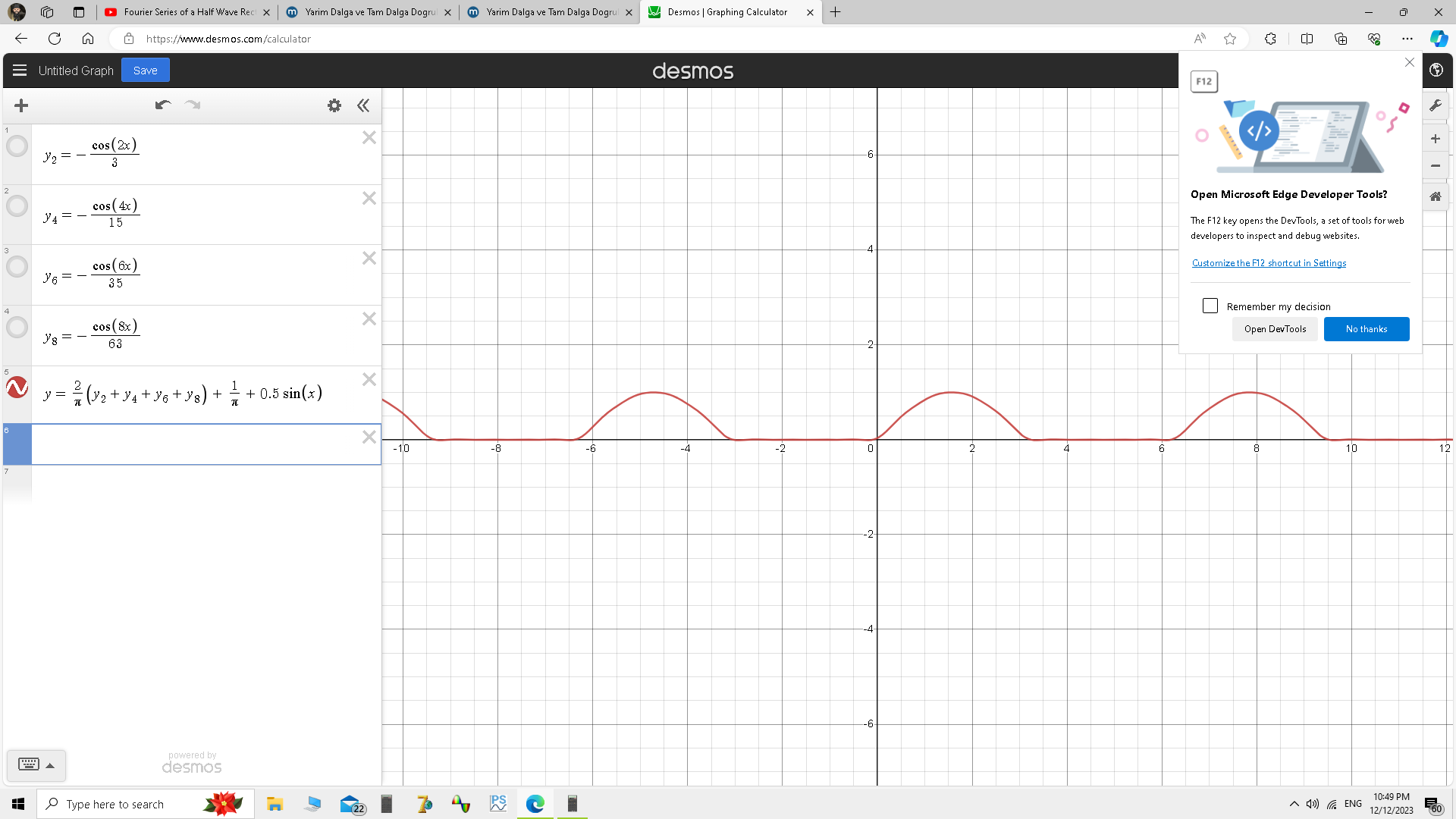
Bunu yarim dalga dogrulttugumuzda
y=sin(x) {x>=0 ....x<pi}
y=0 {x>=pi ..x<2pi}
olarak yazabiliriz.
Bu fonksiyonun Fourier acilimini analitik olarak yapalim. (Dogrudan sonucu veren matematik sitelerinden yardim almak yerine bu islemleri elle yapacagim)
Ancak o kadar hata yapmaya musait ki cozume ulasmam bir kac gunu alabilir.
[math]A_o=\frac{1}{\pi}\int_0^{\pi}sin(\theta)d\theta=\frac{2}{\pi}[/math]
[math]A_n=\frac{1}{\pi}\int_0^{\pi}sin(\theta)cos(n\theta)d\theta[/math]
[math]sin(a+b)=sin(a)cos(b)+sin(b)cos(a)[/math][math]sin(a-b)=sin(a)cos(b) -sin(b)cos(a)[/math][math]sin(a+b)+sin(a-b)=2sin(a)cos(b)[/math][math]sin(a)cos(b)=\frac{1}{2}(sin(a+b)+sin(a-b))[/math][math]A_n=\frac{1}{\pi}\int_0^{\pi}sin(\theta)cos(n\theta)d\theta=\frac{1}{2\pi}\int_0^{\pi}(sin(\theta+n\theta)+sin(\theta-n\theta))d\theta[/math]
[math]A_n=\frac{1}{2\pi}\int_0^{\pi}(sin((n+1)\theta)-sin((n-1)\theta))d\theta[/math][math]A_n=\frac{1}{2\pi}(-\frac{cos((n+1)\theta)}{n+1}+\frac{cos((n-1)\theta)}{n-1})|_0^\pi[/math][math]A_n=\frac{1}{2\pi}(\frac{cos((n-1)\pi) -1}{n-1}-\frac{cos((n+1)\pi)-1}{n+1})[/math]
n tek ise An=0 oluyor. Dolayisi ile An i sadece n cift degerler icin hesaplayacagiz.
[math]B_n=\frac{1}{\pi}\int_0^{\pi}sin(\theta)sin(n\theta)d\theta[/math][math]cos(a+b)=cos(a)cos(b)-sin(a)sin(b)[/math][math]-cos(a+b)=-cos(a)cos(b)+sin(a)sin(b)[/math][math]cos(a-b)=cos(a)cos(b)+sin(a)sin(b)[/math][math]-cos(a+b) + cos(a-b)=2sin(a)sin(b)[/math][math]sin(a)sin(b)=\frac{1}{2}(cos(a-b)-cos(a+b) )[/math][math]sin(x)sin(nx)=\frac{1}{2}(cos(x-nx)-cos(x+nx) )[/math][math]sin(x)sin(nx)=\frac{1}{2}(cos((1-n)x)-cos((1+n)x))[/math][math]B_n=\frac{1}{\pi}\int_0^{\pi}\frac{1}{2}(cos((1-n)\theta)-cos((1+n)\theta))d\theta[/math][math]B_n=\frac{1}{2\pi}\int_0^{\pi}(cos((1-n)\theta)d\theta-\frac{1}{2\pi}\int_0^{\pi}cos((1+n)\theta))d\theta[/math][math]B_n=\frac{1}{2\pi(1-n)}sin((1-n)\theta)|_0^\pi-\frac{1}{2\pi(1+n)}sin((1+n)\theta))|_0^\pi[/math][math]B_n=\frac{1}{2\pi(1-n)}sin((1-n)\pi)-\frac{1}{2\pi(1+n)}sin((1+n)\pi)[/math]
n=1 icin bir terslik var diger tum n degerleri icin Bn katsayisi 0.
n=1 icin ilk integrali cozelim.
[math]B_1=\frac{1}{\pi}\int_0^{\pi}sin(\theta)sin(\theta)d\theta=\frac{1}{2\pi}\int_0^{\pi}(1-cos(2\theta))d\theta=\frac{1}{2}[/math]
Artik herhangi bir n degeri icin An katsayisini dogrudan hesaplayabiliriz.
[math]A_2=-\frac{2}{3\pi}[/math][math]A_4=-\frac{2}{15\pi}[/math][math]A_6=-\frac{2}{35\pi}[/math][math]A_8=-\frac{2}{63\pi}[/math]
[math]y=\frac{A_0}{2}+\sum_{k=1}^{\infin} A_ncos(k\theta)+\sum_{k=1}^{\infin} B_nsin(k\theta)[/math]
Ilk 8 harmonik icin
[math]y=\frac{1}{\pi}+\frac{1}{2}sin(\theta) -\frac{2}{3\pi}cos(2\theta)-\frac{2}{15\pi}cos(4\theta)-\frac{2}{35\pi}cos(6\theta)-\frac{2}{63\pi}cos(8\theta)[/math]
Son düzenleme:
